Artigos | Articles
Vitrúvio e o templo dórico grego: comparando a fonte textual e a evidência arqueológica
Vitruvius and the Greek Doric Temple: comparing the textual source and the archaeological evidence
Vitrúvio e o templo dórico grego: comparando a fonte textual e a evidência arqueológica
Classica - Revista Brasileira de Estudos Clássicos, vol. 34, núm. 1, pp. 31-49, 2021
Sociedade Brasileira de Estudos Clássicos

Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.
Recepción: 11 Octubre 2019
Aprobación: 19 Febrero 2020
Resumo: Vitrúvio atestou no seu tratado De Architectura que aprendeu o seu ofício com os mestres gregos. No livro 4, ensina como deve proceder um arquiteto que deseje construir um templo de ordem dórica. Ele apresenta um esquema de regras que tem como fundamento o módulo, e este deverá ser a medida que padroniza todo o sistema da edificação. Aferir se realmente os templos gregos seguem os seus princípios sempre foi algo que fascinou os arqueólogos, uma vez que as proporções são muito controversas. Objetivamos aqui discutir a descrição histórica do templo dórico e confrontá-la com uma amostra de 63 edifícios (séc. VI-II a.C.). Para isso, abordamos diversas passagens do tratado. Os dados revelam que na amostra temos vários exemplos que atendem às recomendações de Vitrúvio; contudo, esses não se aplicam à maioria dos casos. Isso já era esperado, uma vez que ele apresenta um esquema rígido de concepção, e o tratado foi escrito somente no final da República Romana, ca. 27 a.C.
Palavras-chave: Vitrúvio, templo dórico, arquitetura grega, proporções, módulos.
Abstract: Vitruvius attested in his treatise On Architecture that he learned his trade from the Greek masters. In book 4, he taught how an architect who wishes to build a Doric temple should proceed. He presents a scheme of rules based on the module, which shall be the measure that standardizes the entire building system. Assessing whether Greek temples really follow their principles has always been something that fascinated archaeologists, since the proportions are very controversial. We aim here to discuss the historical description of the Doric temple and to confront it with a sample of 63 buildings (6th-2nd century BC). For this, we have covered several passages of the treaty. The data reveal that in the sample we have several examples that meet Vitruvius’ recommendations; however, they do not apply to most cases. This was already expected, since it presents a rigid design scheme, and the treaty was written only at the end of the Roman Republic, ca. 27 BC.
Keywords: Vitruvius, Doric temple, Greek architecture, proportions, modules.
Introdução
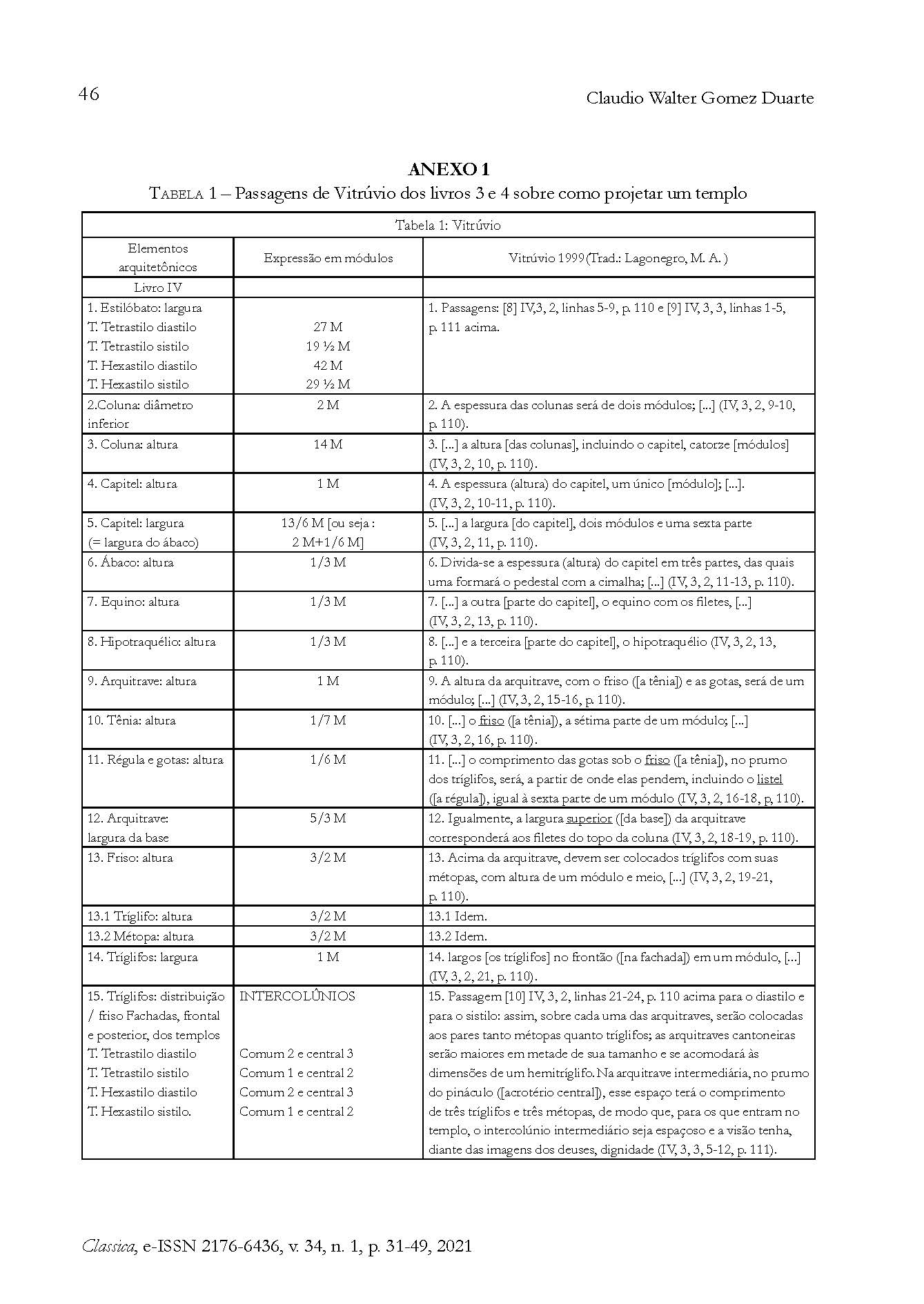
Apresentamos neste artigo uma comparação detalhada entre o tratado De Architectura de Vitrúvio e os templos dóricos gregos, que o autor pretende ensinar a construir a partir de um conjunto de regras que têm como fundamento o módulo. Nossa contribuição para o avanço do debate está nos resultados comparativos obtidos a partir do tamanho da amostra escolhida (63 edifícios) – uma amostra relativamente grande quando comparada com estudos mais recentes, como, por exemplo, Pakkanen (2013) e Wilson Jones (2001, 2018). Percorremos as passagens dedicadas ao assunto e transcrevemos o formulário vitruviano de modo sistemático (vide tabela 1). Na tabela 2, concentramos o banco de dados que nos permite estabelecer a comparação. Como veremos a seguir, a realidade arqueológica mostra que as regras não foram estabelecidas de maneira totalmente mecanizada, como escreveu Vitrúvio, dando margem a variações na decorrência de séculos de aperfeiçoamento e de região para região, e também de acordo com as exigências específicas do local, do culto e da imagem dentro da edificação.
Vitrúvio
Nasceu1 provavelmente ca. 80/70 a.C. Cresceu e educou-se na Campânia ou em Roma. Seu tratado, De Architectura, foi provavelmente escrito e publicado ca. 30/20 a.C. e é considerado a única fonte que chegou até nós sobre arquitetura antiga. Foi fortemente influenciado por fontes gregas creditadas pelo próprio autor. Esse manual aborda questões práticas de modo autoexplicativo, e a formação de seu autor, arquiteto engenheiro militar, pode ter influenciado a maneira de lidar com as abstrações, muito embora a teoria tenha ocupado um lugar relevante em seu programa como um todo (Howe; Rowland, 2001, p. 2; Maciel, 2007, p. 33; Wilson Jones, 2000b, p. 38-39).
Vitrúvio e o templo dórico
Com o parágrafo a seguir, Vitrúvio2 (3, 1, 1) dá início ao tratamento da arquitetura dos templos, o assunto mais extenso do tratado que ocupa os livros terceiro e quarto.
[1]. A composição3 dos templos assenta na comensurabilidade4 [simetria], a cujo princípio os arquitetos deverão submeter-se com muita diligência. A comensurabilidade [simetria] nasce da proporção5 que em grego se diz analogia. A proporção consiste na relação modular6 de uma determinada parte7 dos membros tomados em cada seção ou na totalidade da obra, a partir da qual se define o sistema das comensurabilidades [relações modulares]. Pois nenhum templo poderá ter esse sistema sem conveniente equilíbrio [simetria] e proporção e se não tiver uma rigorosa disposição como os membros de um homem bem configurado8(Maciel, 2007, 3, 1, 1, p. 168).9
Nesta passagem, o autor latino aborda os aspectos teóricos relativos aos edifícios sagrados, independentemente da ordem arquitetônica segundo a qual venham a ser construídos. Vários conceitos compõem a passagem, e para esclarecê-los parece-nos valioso utilizar tanto a tradução de Vitrúvio (Maciel, 2007) como suas notas transcritas para o nosso texto. A interpretação desses conceitos é alvo de inúmeras discussões entre os teóricos da arquitetura, as quais perduram desde o século XV até o presente. Não encontramos lugar aqui para acalorar o debate. Para os nossos propósitos, parece suficiente o próprio texto auxiliado pelas notas. O conceito de simetria ocupa um lugar de destaque na teoria de Vitrúvio, e a melhor chave para o seu entendimento, segundo Wilson Jones, encontra-se no parágrafo [1], onde Vitrúvio explora uma analogia entre a composição do templo e o corpo humano. O interessante dessa passagem, para o nosso estudo, é o marco histórico que situa as bases teóricas inerentes à concepção dos templos que mais se aproximam cronologicamente dos templos gregos. Outra passagem, transcrita no parágrafo [2] a seguir, é a que conecta o conceito de simetria, o sistema modular arquitetônico proposto por Vitrúvio e a metrologia anatômica com os componentes modulares que referenciam a arquitetura do templo jônico (o módulo jônico é a base da coluna) e dórico (o módulo dórico é o tríglifo) (Corso; Romano, 1997, p. 272; Maciel, 2007, p. 25-6; Wilson Jones, 2000a, p. 699; 2000b, p. 41).
[2]. Por sua vez, a comensurabilidade [simetria] consiste no conveniente equilíbrio dos membros da própria obra e na correspondência de uma determinada parte, dentre as partes separadas, com a harmonia do conjunto da figura. Assim como no corpo humano existe a natureza simétrica da euritmia10 a partir do côvado (antebraço), do pé, do palmo e de outras pequenas partes, o mesmo acontece no completo acabamento das obras. Em primeiro lugar, nos templos sagrados, seja pelas espessuras das colunas, seja pelo tríglifo ou mesmo pelo embater;11 [...] (Maciel, 2007, 1, 2, 4, p. 76).12
Nossos interesses sobre a concepção dos templos dóricos encontram seu principal suporte histórico no livro 4 (um dos dez livros que compõem o tratado De Architectura), onde Vitrúvio dá o seu testemunho conforme aprendeu com os mestres gregos (Lagonegro, 1999, 4, 3, 3, linhas 1-2, p. 110), além de fornecer esclarecimentos arquitetônicos de ordem geral:
[3]. [...] Com efeito, da configuração das colunas, fez-se a denominação das três ordens, dórica, jônica e coríntia, das quais a dórica foi a primeira a originar-se, e há muito tempo (Lagonegro, 1999, 4, 1, 3, linhas 14-17, p. 105).13
Vitrúvio situa a origem da coluna dórica como anterior à da coluna jônica, porém não afirma se tratar do templo dórico e sim da coluna. Essa afirmação é difícil de se estabelecer. O dórico é datado de ca. 600 a.C. e o jônico por volta da mesma data ou um pouco posterior (Howe; Rowland, 2001, p. 218). Estudos relativamente recentes sobre os templos no período arcaico revelaram uma concomitância, no tempo e no espaço, ao desenvolvimento das ordens dórica e jônica. Segundo Gros, nem Vitrúvio nem suas fontes teriam acesso a uma reflexão sobre as estruturas arquitetônicas anteriores à colocação do peristilo, situando o arcaísmo para Vitrúvio longe do templo C de Thermos (metade do século VII a.C.). Lembramos também que os primeiros testemunhos da utilização do termo dórico aplicado a uma ordem arquitetônica se encontram na obra de Vitrúvio (Gros, 1992, p. 51-52; Barletta, 2001, p. 83).
[4]. Ora, reinava em toda Acaia e no Peloponeso Doro, filho de Heleno e da ninfa Expétis, que, na antiga cidade de Argos, edificara no terreiro consagrado a Juno [Hera] um templo, por acaso, nessa forma; depois disso, em outras cidades da Acaia, no mesmo gênero, ainda que não houvessem se estabelecido as relações entre as proporções (Lagonegro, 1999, 4, 1, 3, linhas 1-5, p. 105-6).14
Gros chama a atenção para os seguintes aspectos: a diferença entre templum e fanum, o Heraion de Argos, a aparição do templo dórico em Argos e a sua rápida difusão na Grécia (própria) e por último as proporções. Provavelmente Vitrúvio tenha traduzido têmenos por templum e sékos (cela) por fanum – as dificuldades surgem pois estes termos empregados em latim não possuem o mesmo rigor que em grego. O Heraion, templo pentastilo períptero (com número de colunas laterais desconhecido), cela de 33m com opistódomo profundo, colunas inicialmente de madeira com bases de pedra e datado em ca. 590 a.C. por Barletta (2001), constituiu o último passo para a colunata totalmente em pedra. Templos contemporâneos ao Heraion de Argos são de ca. 600-590 e 580 a.C.: o templo de Hera em Olímpia e o templo arcaico de Ártemis em Corfu (Gros, 1992, p. 52).
[5]. Como quisessem colocar colunas nesse templo, desconhecendo suas proporções15 e querendo saber por quais meios poderiam obtê-las, para que fossem apropriadas para suportar as cargas e que tivessem um aspecto de comprovada beleza, mediram a pegada do pé de um homem e relacionaram-na com sua altura. Como encontraram que, no homem, o pé equivale à sexta parte da altura, transportaram a mesma relação para a coluna, e com a espessura que fizeram a base do fuste, exprimiram a altura, inclusive o capitel, em seis vezes ela. Assim, a coluna dórica passou a emprestar aos edifícios as proporções, a firmeza e a beleza do corpo masculino (Lagonegro, 1999, 4, 1, 6, linhas 22-30, p. 106).16
Os dórios, creditados como inventores do dórico, passaram pelo estágio da busca das proporções. Contudo, Vitrúvio se expressa como se eles tivessem consciência de uma definição racional das formas, embora tenham chegado ao dórico por “acaso” (vide passagem [4] acima, linha 3). Em [5], linhas 1-4, faz referência à consolidação do edifício atrelada a uma beleza demonstrável, que seria uma atitude essencialmente racional ancorada no sistema modular. Em seguida, em [5], linhas 4-5, Vitrúvio tenta, não sem alguma ingenuidade, reconstruir a façanha de encontrar as proporções das colunas através de um sistema de medidas anatômicas. Ainda em [5], linhas 5-7, Vitrúvio situa o momento da gênese do sistema modular, sistema este que estabelece um vínculo racional entre o diâmetro inferior da coluna e a sua altura (1:6). Retomando (3, 1, 2), faz a ligação entre as medidas ideais do corpo perfeito com o número perfeito 6. As evidências arqueológicas mostraram que o esquema 1:6 (ou seja, aproximado) só foi utilizado tardiamente na Grécia, entre os séculos V e IV a.C. (por exemplo: o templo de Apolo em Delfos (1:5,86), o templo de Atena em Tegeia (1:6,07) e o templo de Zeus em Nemeia (1:6,35), entre outros, enquanto os templos dóricos arcaicos dos século VI a.C. apresentam proporções mais robustas (por exemplo: o templo de Apolo em Siracusa (1:3,8), o Heraion de Olímpia (1:4,17), o templo de Ártemis em Corfu (1:4,9) e outros). No entanto, em raros exemplares das mais antigas criações dóricas encontram-se proporções próximas das de Vitrúvio (1:6), como é caso da tholos arcaica de Delfos. Em [5], linhas 9-10, Gros chama a atenção para a passagem do livro 1 – Para Minerva, Marte e Hércules, construam-se edifícios dóricos – que se soma à explicação da “virilidade” do dórico e sua adequação às divindades masculinas ou guerreiras (Gros, 1992, p. 62-3; Lagonegro, 1999, 1, 2, 5, linhas 7-8, p. 55).
[6]. Já os pósteros, aperfeiçoados na elegância e no refino dos julgamentos, e encantados com as medidas mais graciosas, definiram a altura da coluna dórica em sete vezes o diâmetro da espessura, e o da jônica, em nove (Lagonegro, 1999, 4, 1, 8, linhas 12-15, p. 106).17
Em [6], o sistema vitruviano confere aos traços masculinos do dórico e aos femininos do jônico um papel notável, e faz uma distinção entre os “inventores” e os “refinadores” das ordens. Essa passagem está permeada da noção de progresso aristotélico (difundido na cultura latina por Posidônio), onde há a aplicação do esquema de evolução humana a uma τέχνη. No final da passagem [6], Gros chama a atenção para o fato de que não são os módulos que diminuem, mas sim as relações modulares que mudam. A modificação progressiva das ordens acarretou diversos problemas corretivos aos edifícios. Observa também que a passagem entre as proporções 1:6 e 1:7 não se faz de modo linear, como por exemplo entre o templo de Atena em Tegeia (1:6,07) e o templo de Atena Políade em Pérgamo (1:6,97) (Gros, 1992, p. 71). Para Howe e Rowland, a passagem [6], linhas 3-4, corresponde ao desenvolvimento da arquitetura grega; eles observam que a altura da coluna dórica em relação ao diâmetro inferior se estabeleceu de modo geral entre 1:4 ½. e 1:5 no século V. No século IV e no período helenístico chegaram a 1:6 e 1:7. Howe e Rowland apontam a principal correção ao esquema vitruviano para a primeira geração do dórico (600-570 a.C.), onde as proporções variaram entre colunas bem espessas e colunas bem esbeltas. Mudanças nas artes figurativas se verificaram também no século IV (por exemplo, quando comparados os cânones de Policleto e Lísipo) (Howe; Rowland, 2001, p. 213).
[7]. Alguns arquitetos antigos discordaram da conveniência de se construir templos na ordem dórica, porque nos edifícios desse gênero suas proporções apresentavam-se incorretas e contraditórias. Assim, negou-o Arcésio, bem como Pítio e não menos Hermógenes. [...] Todavia, não porque seu aspecto ou dignidade na forma carecessem de elegância, mas porque a distribuição dos tríglifos e ornamentos em estuque na obra é carregada18 e desagradável (Lagonegro, 1999, 4, 3, 1, linhas 1-4, 7-9, p. 109-10).19
Pode-se verificar realmente que na própria Grécia, e principalmente na Ásia (onde praticamente esta ordem nos templos foi pouco adotada), ocorreu um progressivo abandono da ordem dórica a partir do final do século IV a.C., se levarmos em consideração que no século IV a.C. foram construídos vinte e um templos dóricos e no século III a.C. aproximadamente cinco, dos quais temos certeza em relação a três (Atena Políade em Pérgamo, Asclépio em Messena e o templo de Atena em Troia). Já no século II a.C., foram apenas três (o templo de Asclépio em Cós, e de Hera em Pérgamo e possivelmente o de Zeus em Levadia). Para Gros, esse abandono da ordem dórica não está ligado, como sugere Vitrúvio, ao gosto dos arquitetos, mas sim ao fato de o dórico, embora célebre, não atender mais às exigências da nova arquitetura helenística. Os raros templos dóricos construídos no período helenístico são estruturas arcaizantes que, por motivos religiosos ou políticos, fazem referência aos modelos clássicos. Em relação às razões atribuídas aos entraves modulares que a ordem dórica proporciona, destaca-se o conflito dos tríglifos de ângulos do friso. Além disso, o abandono da ordem estaria mais ligado às desvantagens estruturais – as dimensões robustas do entablamento dórico exigem uma menor amplitude entre as colunas. O período helenístico caracteriza-se pela tendência ao alargamento dos intercolúnios e por uma leveza maior nos entablamentos. Em [7], linhas 3-4, Vitrúvio faz referência a arquitetos e teóricos gregos desde o fim do século IV até o final do III a.C., um período de sistematização e reflexão sobre ordens marcado pelo questionamento teórico e desapego à ordem dórica. Em [7] ainda, linhas 4-7, Vitrúvio relembra a excelência e o prestígio do templo dórico por várias gerações na Grécia, tanto em termos religiosos quanto arquitetônicos, e retoma os problemas de comensurabilidade ou de coerência modular exemplificados pelas questões decorrentes da distribuição dos tríglifos e métopas no friso (Gros, 1992, p. 117-21).
[8]. Porém, é necessário que os tríglifos sejam colocados diante dos quadrantes intermediários das colunas; que as métopas que estão entre os tríglifos sejam executadas tão largas quanto altas. E os tríglifos diante das colunas cantoneiras, que se executem nas partes extremas, não distante dos quadrantes intermediários. Assim, as métopas que forem executadas próximas aos tríglifos cantoneiros não serão quadrangulares, mas oblongadas em metade da largura do tríglifo. Mas os que quiserem executar métopas todas com igual medida, diminuirão os intercolúnios extremos em metade da largura do tríglifo. Esse aspecto, que se obtém ou por alongamento das métopas ou por contração dos intercolúnios, é incorreto. Por esse motivo, pareceu necessário aos antigos evitar as relações das proporções20 dóricas nos edifícios sacros (Lagonegro, 1999, 4, 3, 2, linhas 9-20, p. 110).21
Vitrúvio enuncia aqui um princípio que remete à lógica estrutural dos templos em madeira, pois os tríglifos “eram” a extremidade do vigamento do telhado e, portanto, deveriam apoiar-se no eixo das colunas. Na passagem [8] ele omite o verdadeiro problema que leva à descontinuidade do ritmo do friso (tríglifo-métopa), que se deve ao seguinte fato: no templo de pedra, a largura do tríglifo é menor que a largura da arquitrave – por motivos estruturais – e no templo de madeira essas larguras coincidem, não havendo necessidade de abrir mão do princípio nas extremidades das fachadas. Os conflitos de continuidade no friso foram investigados pela primeira vez em 1899 e, desde então até o presente (Osthues, 2005, p. 1-154), foram muito estudados por renomados pesquisadores. Em [8], linhas 4-8, temos as consequências imediatas geradas pelo não alinhamento do tríglifo de ângulo, que resultam em duas opções: ou alongamos a métopa e mantemos o intercolúnio normal, ou mantemos a métopa normal e reduzimos o intercolúnio. O primeiro caso é o mais comum, mas há exemplos para o segundo caso (como o Olimpieion de Agrigento). Verificou-se uma tendência na arquitetura siciliana arcaica de modificar o ritmo do friso e manter o intercolúnio constante, e uma tendência contrária na arquitetura clássica na Grécia metropolitana. A grande discussão reside no valor atribuído por Vitrúvio ao alargamento das métopas de ângulo, que está em desacordo com a sua própria teoria, embora se verifiquem casos reais onde isso ocorre. Nas linhas 8-11 da passagem [8], Vitrúvio deixa transparecer uma conotação moral atribuída aos defeitos da obra arquitetônica e à necessidade de um compromisso estrutural ou modular (Gros, 1992, p. 121-4).
[9]. Nós, por outro lado, expusemos, como determina o método, conforme aprendemos com os mestres, de tal modo que, se alguém quiser proceder em atenção a essas determinações, encontre explicadas as relações com as quais poderá realizar à perfeição os edifícios sacros ao modo dórico, corrigidos e sem defeitos (Lagonegro, 1999, 4, 3, 3, linhas 1-5, p. 110).22
Vitrúvio, em consenso com os arquitetos do helenismo e seus contemporâneos em relação aos problemas que permeiam a ordem dórica, assume a tarefa de organizar as relações modulares, e em [9] anuncia que, apesar do abandono gradativo da ordem dórica, apresentará uma metodologia racional baseada no ensinamento dos mestres (embora coloque contribuições pessoais, sobretudo com a intenção de solucionar os problemas relativos ao friso dórico), a qual superaria as contradições modulares da ordem dórica (Falus, 1979, p. 268). Segundo Gros (1992, p. 126 e XXI), “Tout se passe comme si le théoricien se donnait ici le simple plasir de déveloper um programme rationnel dont il sait qu’en réalité il n’a jamais été appliqué, ou au moins dont il n’a aucunement l’intention de faire l’épreuve concrète”.
[10]. A fachada do templo dórico, no local onde forem colocadas as colunas, se vier a ser tetrastila, será dividida em vinte e sete partes; se hexastila, em quarenta e duas. Dessas partes, uma será tomada como módulo, que em grego se diz εμβατηρ, e do arranjo desse módulo se conseguirá, por meio de cálculos, sua distribuição por toda a obra (Lagonegro, 1999, 4, 3, 3, linhas 5-9, p. 110).23
[11]. Por outro lado, se a obra tiver de ser realizada segundo o modo sistilo e monotríglifo, a fachada do templo, se for tetrastila, será dividida em dezenove partes e meia; se hexastila, em vinte e nove e meia. Dessas partes, uma será adotada como módulo, segundo o qual se o dividirá, tal como foi descrito acima (Lagonegro, 1999, 4, 3, 7, linhas 1-5, p. 111).24
Nas passagens [10] e [11], Vitrúvio define como será deduzido o módulo para cada tipo de templo. Vitrúvio leva em consideração apenas a fachada, e sugere que a largura do templo seja um dado a partir do qual o arquiteto deve organizar a sua planta (Gros, 1992, p. 126).
[12]. [...] divididos [distribuídos] [os tríglifos] de forma que estejam dispostos nas colunas cantoneiras e intermediárias sobre seus quadrantes médios; nos intercolúnios [comuns], aos pares, e nos intercolúnios intermediários [ou seja, centrais], tanto anteriores [do pronaos] quanto posteriores, em número de três [distribuição estabelecida para as fachadas hexastilas dóricas diastilas] (Lagonegro, 1999, 4, 3, 4, linhas 21-4, p. 110).25
Vitrúvio expõe em [11] e [12] como se deve proceder para compor o friso, e propõe para essa ordem arquitetônica quatro fachadas diferentes: o templo tetrastilo diastilo, o hexastilo diastilo, o tetrastilo sistilo e o hexastilo sistilo. Em termos de organização da planta, as prescrições de Vitrúvio conduzem ao tipo pronaos e cela (Lagonegro, 1999, 4, 3, 4 e 7 p. 110-11):
-
Templo tetrastilo diastilo: 2 intercolúnios comuns com 2 tríglifos entre as colunas e o intercolúnio central com 3 tríglifos entre as colunas
-
Templo tetrastilo sististilo: 2 intercolúnios comuns com 1 tríglifo entre as colunas e o intercolúnio central com 2 tríglifos entre as colunas;
-
Templo hexastilo diastilo: 4 intervalos comuns com 2 tríglifos entre as colunas e o intervalo central com 3 tríglifos entre as colunas;
-
Templo hexastilo sistilo: 4 intervalos comuns com 1 tríglifo entre as colunas e o intervalo central com 2 tríglifos entre as colunas.
As passagens seguintes, nas quais Vitrúvio expõe a composição completa das fachadas, são sistematizadas na tabela 1, após as referências bibliográficas (Lagonegro, 1999, livro IV, 3, p. 110-11). Vitrúvio opta por espaços mais generosos entre as colunas para os templos diastilos, adotando, em vez do sistema monotríglifo tradicional, o sistema de dois e três tríglifos entre as colunas. Mantém para os templos sistilos o sistema monotríglifo, exceto para o espaçamento central entre as colunas, composto de dois tríglifos. Ademais, escolhe uma tipologia que teve sua origem nos pórticos e nos propileus. Os propileus clássicos da Acrópole de Atenas se assemelham à fachada do hexastilo sistilo. Disposições semelhantes serão encontradas apenas em templos do período helenístico, e a partir do século III. O templo de Atena Políade em Pérgamo, hexastilo, apresenta uma distribuição de tríglifos semelhante ao hexastilo diastilo, porém no espaçamento central possui dois tríglifos, e não três. Ainda em solo grego, o templo de Zeus em Pérgamo se assemelha ao tetrastilo diastilo. Com a mesma restrição que o exemplo anterior, no espaçamento central possui dois tríglifos em vez de três. Na Itália, o templo tetrastilo dórico de Cora, ca. 80 d.C., apresenta o sistema de três tríglifos entre todos os intervalos, o que difere também do tetrastilo diastilo nos intercolúnios laterais. Não podemos esquecer, ainda, que nenhum dos exemplos acima possui o sistema de tríglifo de ângulo proposto por Vitrúvio:
[13]. Colocados dessa forma os tríglifos, as métopas que estiverem entre eles serão tão altas quanto longas, bem como, nos ângulos extremos, serão estampadas hemimétopas com largura de meio módulo. Que assim seja, de modo que sejam corrigidos todos os defeitos das métopas, intercolúnios e lacunas que serão executadas igualmente moduladas (Lagonegro, 1999, 4, 3, 5, linhas 6-9, p. 111).26
O princípio da meia-métopa encontrou aplicação entre as construções desde o renascimento até o neoclássico no século XIX (Gros, 1992, p. 132-3, 137, XLVII). Desconhecem-se para a Antiguidade templos dóricos que atendam ao receituário vitruviano. Para Falus, as análises dos templos dóricos helenísticos são evidências de que Vitrúvio não deduziu suas regras da prática arquitetônica, e sim as formulou de modo especulativo. Frézouls (1985) chama a atenção para as análises de Wesenberg (1983), que mostra que o templo vitruviano não faz referência a nenhuma realidade arquitetônica, em nenhuma época.
Embora as comparações dos templos vitruvianos não tenham encontrado até o momento suporte material para validá-los como um todo, seja em termos proporcionais ou tipológicos de modo estrito, há exemplos, como vimos acima, onde encontram-se paralelos pelo menos em alguns elementos arquitetônicos de certos edifícios. O sistema ou princípio modular de composição arquitetônica vitruviana trouxe boas pistas para o entendimento da concepção dos templos dóricos. Com algumas modificações do sistema modular, Wilson Jones (2001) encontra uma interpretação plausível para dez templos dóricos do período clássico, proposta duramente rebatida por Jari Pakkanen. Para este autor, outros elementos arquitetônicos teriam maior probabilidade que o tríglifo de ser o módulo do edifício dórico (Falus, 1979, p. 270; Frézouls, 1985, p. 226; Pakkanen, 2013; Wilson Jones, 2001, p. 675-713).
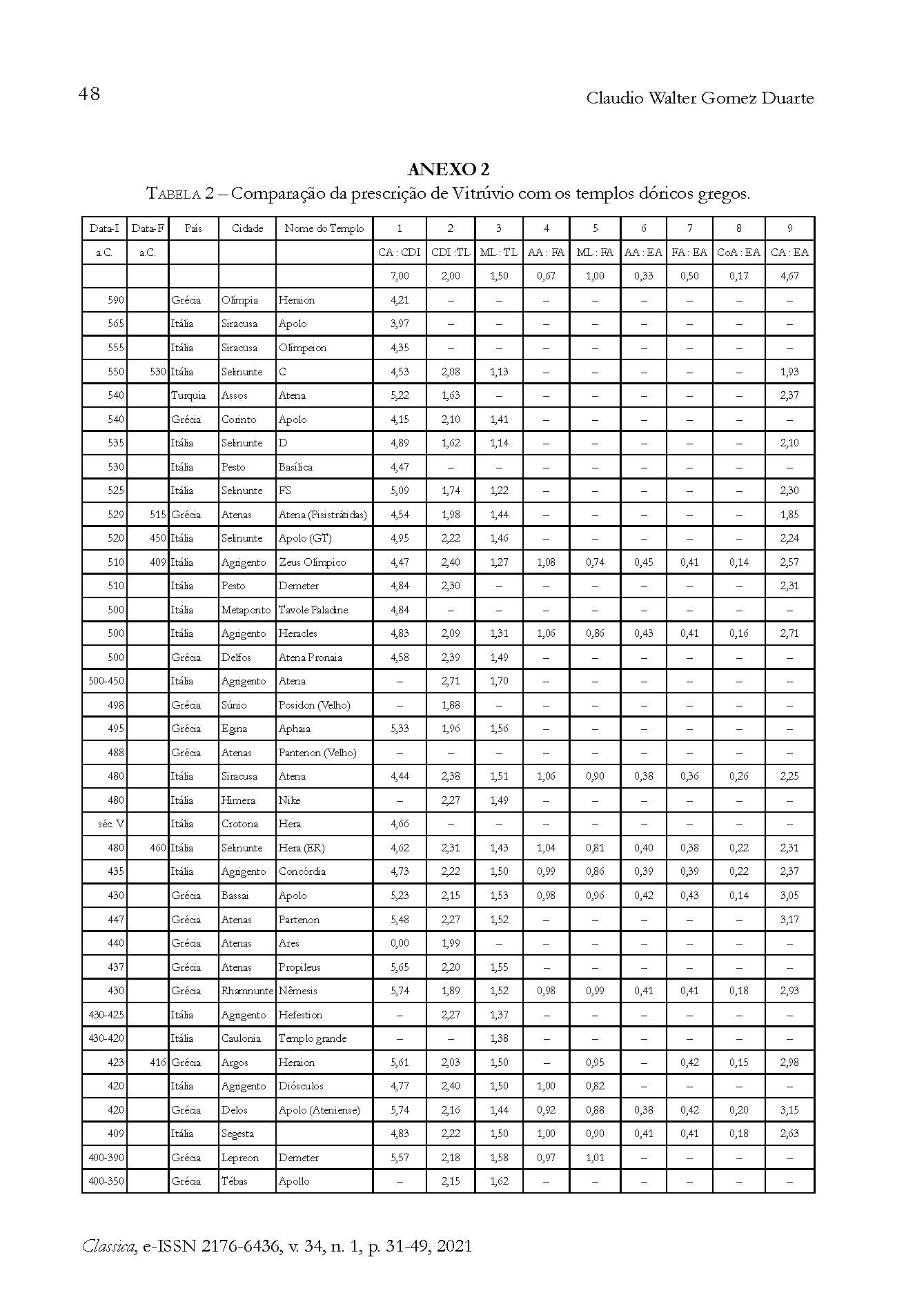
Sem dúvida, a comparação é uma das ferramentas mais poderosas que o arqueólogo possui no seu trabalho. Para entendermos melhor em que medida o testemunho histórico de Vitrúvio se distancia ou se aproxima da realidade arqueológica dos templos dóricos, preparamos a tabela 2 (Anexo 2), na qual é possível comparar algumas proporções recomendadas por Vitrúvio com as proporções que se verificaram nos templos dóricos gregos. Na tabela 1 (Anexo 1) sintetizamos as recomendações de Vitrúvio para a composição dos templos dóricos e escolhemos nove relações dentre seus elementos, gerando o quadro comparativo da tabela 2. Na tabela 2, linha 3, os valores indicam a proporção que Vitrúvio recomenda. Nas linhas abaixo, encontramos a proporção correspondente para cada templo grego. Esses valores são os nossos parâmetros para comparar as proporções dos templos dóricos gregos com as proporções dos templos dóricos vitruvianos.
A seguir, abreviaturas para a tabela 2:
1. CA: CDI Coluna, Altura : Coluna, Diâmetro Inferior
2. CDI : TL Coluna, Diâmetro Inferior : Triglifo, Largura
3. ML : TL Métopa, Largura : Tríglifo, Largura
4. AA : FA Arquitrave, Altura : Friso, Altura
5. ML : FA Métopa, Largura : Friso, Altura
6. AA : EA Arquitrave, Altura : Entablamento, Altura
7. FA : EA Friso, Altura : Entablamento, Altura
8. CoA : EA Cornija, Altura : Entablamento, Altura
9. CA : EA Coluna, Altura : Entablamento, Altura
Na tabela 2, podemos apreciar um número maior de exemplos para a primeira comparação – a relação entre a altura da coluna e o seu diâmetro inferior (coluna 1, CA:CDI, tab. 2), já discutida acima. Salientamos que, ao comparar as proporções obtidas na tabela 2, linha 1, com os dados acima para a mesma discussão, podemos observar dados um pouco diferentes para o mesmo templo. É comum nos depararmos com situações como essa, pois ao lidarmos com fontes diferentes obtemos discrepâncias nos resultados. O exemplo mais notável é a proporção acima dada para o templo de Atena em Tegeia por Pierre Gros, em 1992 (oriunda de Mertens, 1984, p. 134), de 1:6,07, se comparada com a da tabela 2 que é de 1:6,51 (fornecida por Østby, 1992, tab. I e II); Dinsmoor (1950) fornece para o mesmo templo a proporção 1:6,11. Østby pode estar baseado em descobertas mais recentes, ou foi um erro de publicação? Fatos como esse chamam-nos a atenção para a necessidade de cautela na manipulação de dados. A proporção fornecida por Østby coloca o templo de Tegeia, ca. 350 a.C., próximo do templo de Atena em Troia, anterior a 281 a.C. (1:6,50). A seguir, Vitrúvio recomenda que o diâmetro inferior da coluna seja composto de dois módulos, ou a largura de dois tríglifos. Corso e Romano observam que essa relação 1:2 se estabelece de modo frequente na arquitetura templária dórica (Corso; Romano, 1997, p. 469). De fato, ao analisarmos a coluna 2 (CDI:TL, tab. 2) vemos vários exemplos que se aproximam dessa proporção, principalmente para os períodos clássico e helenístico, com alguns exemplos também para o período arcaico. Para uma análise mais precisa, poderíamos estabelecer parâmetros de tolerância para apurar as aproximações. Em 3 (ML:TL, tab. 2), a relação entre a largura da métopa e do tríglifo está na proporção 3:2 ou 1:1,50. Bundgaard observa que, a partir da metade do século V a.C., a proporção recomendada por Vitrúvio (3:2) se fixa e se verifica de forma recorrente pelo menos na maioria dos edifícios conhecidos (Bundgaard, 1957, n. 254). Em 3 (ML:TL, tab. 2) podemos verificar vários exemplos onde isso acontece (próximos de 1,5), e inclusive alguns exemplos para o período anterior a 450 a.C. Em 4 (AA:FA, tab. 2) Vitrúvio prescreve a proporção entre a arquitrave e o friso (AA = 2/3 FA ou 0,67 FA). Gros chama a atenção para o fato de que arquitraves tão leves em relação ao friso só encontram paralelos nos edifícios dóricos do período republicano romano. Se consultarmos a tabela 2 não encontraremos nenhum exemplo com essa proporção (Gros, 1992, p. 130). Temos para o século V a.C. proporções em torno de 1 e para os séculos IV e III proporções em torno de 0,90. O valor que se aproxima mais é do século II: 0,72 em Pérgamo. Em 5 (ML:FA, tab. 2), Vitrúvio propõe uma métopa quadrada, pois a relação entre a base e a altura é 1:1 (ML=FA). Analisando os números da coluna 5, percebemos que a maioria das métopas tendem a ser quadradas e que algumas chegam a ser realmente assim. O entablamento dórico se compõe de arquitrave, friso e cornija. Para entender melhor como se distribuem esses elementos no entablamento, criamos as colunas 6, 7 e 8. Vitrúvio propõe que 33% da altura do entablamento corresponda à arquitrave (AA=1/3EA), 50% ao friso (FA= ½ EA) e 17% à cornija (CoA=1/6 EA). Ao analisarmos as colunas 6, 7 e 8, percebemos que a distribuição vitruviana não atende simultaneamente à composição dos entablamentos dóricos, embora haja exemplos isolados onde a arquitrave chega perto de 33% – como é o caso do templo de Déspoina, Licosura, 175-150 a.C., no qual ocupa-se 32% do entablamento. Para o friso encontramos exemplos com diferenças em torno de 5% a partir do século IV a.C. A cornija em torno de 17% do entablamento, como estabelece Vitrúvio, encontra vários exemplos a partir do século V a.C. Por último, na coluna 9 (CA:EA) a relação entre a altura da coluna e o entablamento é dada por CA=14/7EA. Encontramos na tabela 2 casos isolados com proporções próximas daquelas que Vitrúvio recomenda: Troia e Pérgamo no século III a.C.
Considerações finais
Em suma, no livro 4, Vitrúvio estabelece para a concepção do templo de ordem dórica um sistema proporcional baseado numa única unidade básica, o módulo (ou a largura do tríglifo). Apresenta, portanto, um sistema modular no qual todos os elementos arquitetônicos da edificação são dimensionados como múltiplos ou frações desse módulo. Fornece desta forma um conjunto de regras que definem cada elemento arquitetônico do templo dórico vitruviano – que, como vimos, conduz a quatro tipos diferentes, sem equivalentes estritos na arquitetura grega. Foram testadas nove relações proporcionais entre os elementos arquitetônicos nos templos, como mostra a tabela 2. Coletamos os seguintes resultados para a nossa amostra de 63 templos: CA:CDI (7,00) – 10 templos para proporções entre 1:6 e 1:7; CDI:TL (2) – 19 templos com uma margem de erro de ±5%; ML:TL (1,5) – 38 templos com uma margem de erro de ± 5%; AA:FA (0,67) – 1 templo com uma margem de erro de 7,46%; ML:FA (1,00) – 19 templos com uma margem de erro de ±10%; AA:EA (0,33) – 20 templos com uma margem de erro de ±25%; FA:EA (0,50) – 23 templos com uma margem de erro de -20%; CoA:EA (0,17) – 16 templos com uma margem de erro de ±15%; CA:EA (4,67) – 9 templos com uma margem de erro de ±25%. Analisando os resultados, observamos que comparar os templos dóricos gregos com o sistema modular de Vitrúvio nos leva inevitavelmente, em algumas instâncias, a grandes aproximações. Como vimos, é difícil estabelecer um único critério para cada proporção; contudo, algumas relações se aproximam mais, outras menos. Concordamos com a afirmação de Wilson Jones (2001, p. 700): “ele [Vitrúvio] nunca está totalmente certo, mas nunca está totalmente errado”. Devemos levar em consideração que, mesmo sendo uma fonte excepcional para a história da arquitetura na Antiguidade, trata-se de um texto que não foi contemporâneo ao desenvolvimento da ordem dórica, sendo uma compilação tardia de uma tradição. De Architectura é uma obra de valor inestimável, a qual nos permite acessar, mesmo que de maneira indireta, a concepção dos templos de ordem dórica grega.
Referências
Referências
CORSO, Antonio; ROMANO, Elisa (trad.) Vitruvio. De architettura. A cura di P. Gros. Torino: Einaudi, 1997.
GRANGER, Frank (trad.) Vitruvius. On architecture: Books 1-5. Cambridge: Harvard University Press, 1955. v. 1.
GROS, Pierre (trad.) Vitruve. De l’Architecture: Livre IV. Texte établi, traduit et commenté par P. Gros. Paris: Les Belles Lettres, 1992.
GROS, Pierre (ed.) Vitruve. De l’Architecture. Texte établi, traduit et commenté par P. Gros. Paris: Les Belles Lettres, 2015.
HOWE, Thomas Noble; ROWLAND, Ingrid (trad.) Vitruvius. Ten books on Architecture. Cambridge: Cambridge University Press, 2001 [1999].
LAGONEGRO, Marco Aurélio (trad.) Vitrúvio. Da Arquitetura. São Paulo: Hucitec, 1999.
MACIEL, M. Justino (trad.) Vitrúvio. Tratado de Arquitetura. São Paulo: Martins Fontes, 2007. 1a ed. 2006.
BARLETTA, Barbara. The origins of Greek architectural orders. Cambridge: University Press, 2001.
BUNDGAARD, Andreas Jens. Mnesicles, a Greek architect at work. Copenhague: Gyldendal, 1957.
DINSMOOR, William Bell. The architecture of ancient Greece. London: B. T. Batsford, 1950.
FALUS, Robert. Sur la théorie de module de Vitruve. Acta archaeologia academiae scientiarum hungaricae, v. 31, p. 249-270, 1979.
FRÉZOULS, Edmond. Vitruve el le dessin d’architecture. In BOMMELAER, Jean-François (org.). Le dessin d’architeture dans les sociétés antiques. Colloquium, Strasbourg 26-28 janvier 1984. Strasbourg: Université des Sciences Humaines de Strasbourg, 1985, p. 213-29.
GRUBEN, Gottfried. Griechische Tempel und Heiligtümer. München: Hirmer, 2001.
HOLLAND, Leicester Bodine. The origin of the Doric entablature. American Journal of Archaeology, n. 21, p. 117-158, 1917.
MERTENS, Dieter. Città e monumenti dei greci d’occidente. Dalla colonizzazione alla crisi di fine V secolo a.C. Roma: L’Erma di Bretschneider, 2006.
MERTENS, Dieter. Der Tempel von Segesta und die dorische Tempelbaukunst des griechischen Westens in klassischer Zeit. Mainz am Rhein: Philipp von Zabern, 1984.
OSTHUES, Ernst-Wilhelm. Studien zum dorischen Eckkonflikt. Jahrbuch des Deutschen Archäologischen Instituts, v. 120, p. 1-154, 2005.
ØSTBY, Erik. Dorische Tempel von Pherai. Opuscula Atheniensia: Annual of the Swedish Institute at Athens, v. 19, p. 85-113, 1992.
PAKKANEN, Jari. Classical Greek architectural design: A quantitative approach. Helsinki: Foundation of the Finnish Institute at Athens, 2013.
SPAWFORTH, Tony. The complete Greek temples. London: Thames & Hudson, 2006.
TOMLINSON, Richard A. The doric order: Hellenistic Critics and Criticism. Journal of Hellenic Studies, v. 83, p. 133-45, 1963.
WILSON JONES, Mark. Approaches to Architectural Proportion and the “Poor old Parthenon”. In COHEN, Matthew A.; DELBEKE, Maarten (ed.). Proportional systems in the history of architecture. A critical reconsideration. Leiden: Leiden University Press, 2018, p. 199-231.
WILSON JONES, Mark. Doric measure and architectural design 1: The evidence of the relief from Salamis. American Journal of Archaeology, n. 104, p. 73-93, 2000a.
WILSON JONES, Mark. Doric measure and architectural design 2: A modular reading of the classical temple. American Journal of Archaeology, n.105, p. 675-713, 2001.
WILSON JONES, Mark. Principles of Roman architecture. New Haven: Yale University Press, 2000b.
ANEXO 1
ANEXO 2

Holland (1917); Dinsmoor (1950); Bundgaard (1957); Lehmann (1960); Tomlinson (1963); Coulton (1974); Mertens (1984, 2006); Østby (1992); Gruben (2001); Spawforth (2006), passim. Planilha, montagem nossa
Notas
